
https://school.programmers.co.kr/learn/courses/30/lessons/181186
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제
정우는 예술적 감각이 뛰어난 타일공입니다. 그는 단순한 타일을 활용하여 불규칙하면서도 화려하게 타일링을 하곤 합니다.
어느 날 정우는 가로 길이 n, 세로 길이 3 인 판을 타일링하는 의뢰를 맡았습니다. 아방가르드한 디자인 영감이 떠오른 정우는 다음과 같은 두 가지 종류의 타일로 타일링을 하기로 결정했습니다.
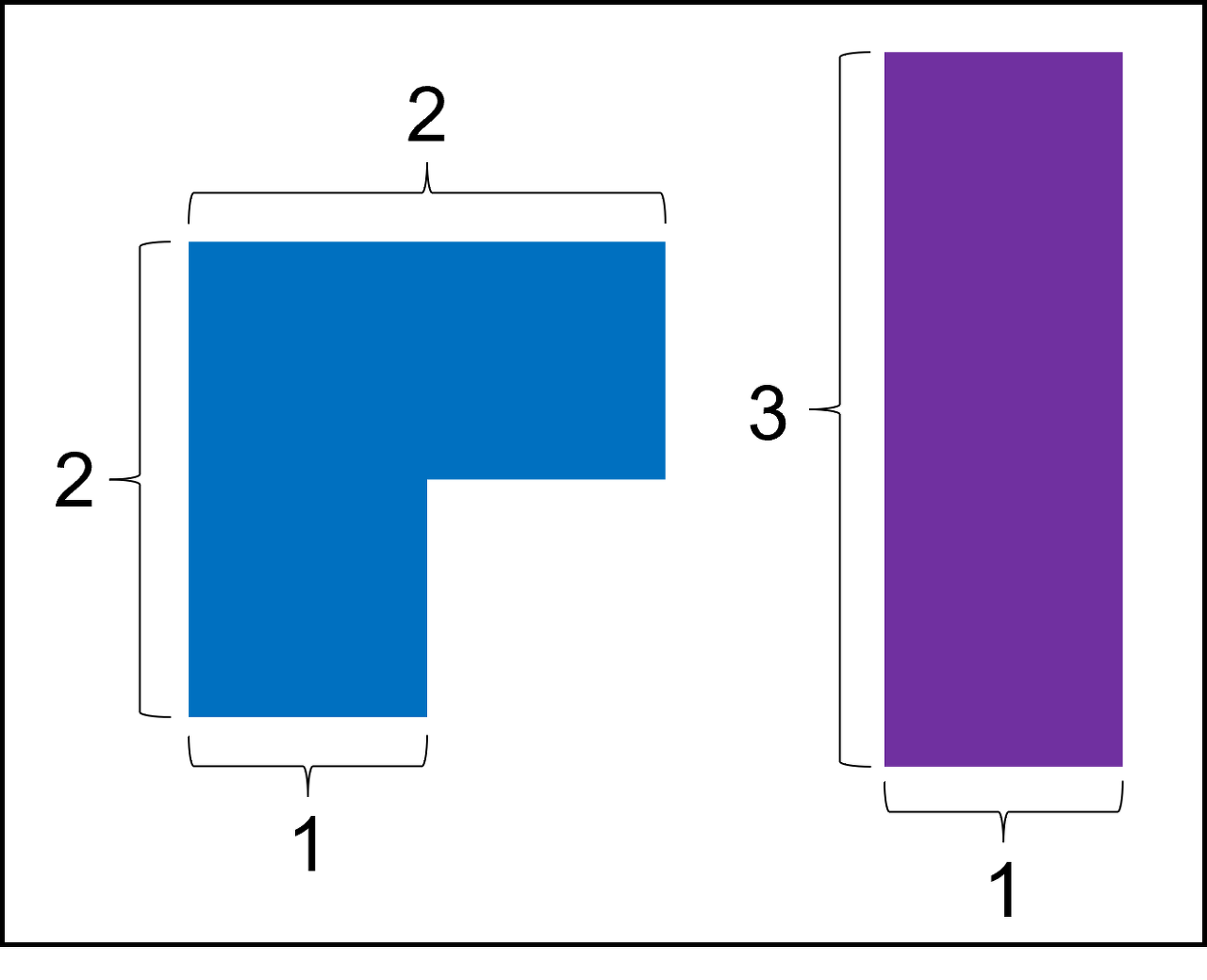
각 타일은 90도씩 회전할 수 있으며 타일의 개수는 제한이 없습니다.
n이 주어졌을 때, 이 두 가지 종류의 타일로 n x 3 크기의 판을 타일링하는 방법의 수를 return 하도록 solution 함수를 완성해주세요.
입출력( + 추가적인 Test Case)
| n | result |
| 1 | 1 |
| 2 | 3 |
| 3 | 10 |
| 4 | 23 |
| 5 | 62 |
| 6 | 170 |
| 7 | 441 |
제한사항
- 1 ≤ n ≤ 100,000
- 결과는 매우 클 수 있으므로 1,000,000,007 로 나눈 나머지를 return합니다.
풀이방법
정말 정말 힘들었습니다.... 정말 힘들었어요.. 정말로... 이상한 패턴 찾느라 고생했습니다...

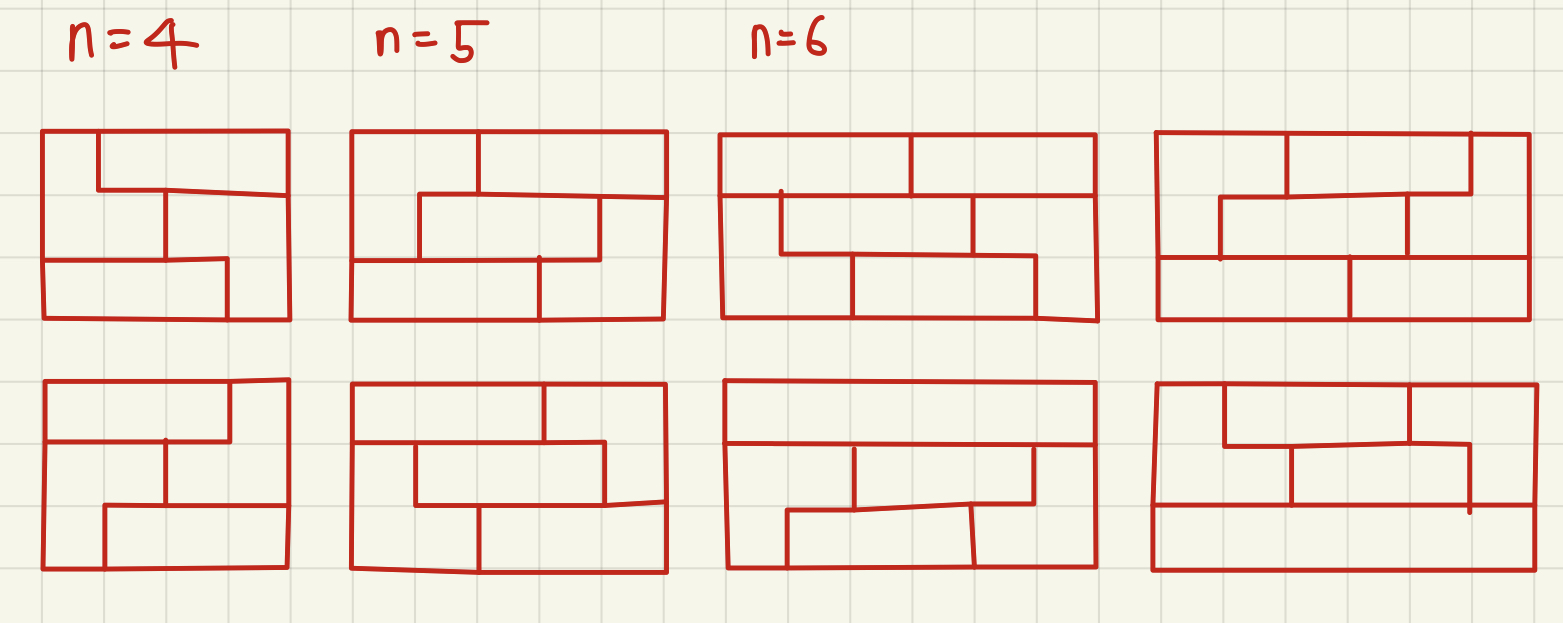
이러한 패턴들을 찾아낸 뒤, dp를 이용해 풀었습니다.
n <= 6 일 때까지 값을 각각 dp 배열과 sum_dp 배열을 만들어 준뒤 n >= 7 부터 반복문을 통해 계산했습니다.
dp[n]에 대해 n-1, n-2, n-3 은 각각 1, 2, 5를 곱해서 더해주면 됩니다. 하지만 n-4, n-5, n-6은 계속 unique한 모양이 생깁니다. n = 7일 때, n=4 인 경우에 1*3막대를 가운데에 추가해야하기 때문입니다.
다시 말해서 3의 배수로 unique한 패턴이 생기기 때문에 누적 합을 저장할 배열(sum_dp) 필요합니다.
그래서 sum_dp[i] 는 dp[i]와 3의 배수로 증가하는 unique한 타일인 sum_dp[i-3]을 더해주면서 저장해줍니다.
코드
def solution(n):
dp = [0 for _ in range(100001)]
# 누적 합
sum_dp = [0 for _ in range(100001)]
sum_dp[1] = 1
sum_dp[2] = 3
sum_dp[3] = 11
sum_dp[4] = 24
sum_dp[5] = 65
sum_dp[6] = 181
dp[1] = 1
dp[2] = 3
dp[3] = 10
dp[4] = 23
dp[5] = 62
dp[6] = 170
for i in range(7, n+1):
dp[i] = dp[i - 1] + dp[i - 2] * 2 + dp[i - 3] * 5 + sum_dp[i - 4] * 2 + sum_dp[i - 5] * 2 + sum_dp[i - 6] * 4
dp[i] = dp[i] % 1000000007
# 누적 합 계산
sum_dp[i] = dp[i] + sum_dp[i-3]
sum_dp[i] = sum_dp[i] % 1000000007
return dp[n]결론
어렵다. 진짜 어렵다... 누적 합에 대해 다시 공부하거나 점화식에 대해 공부해봐야겠다.
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] [Python] (Level 3) 부대복귀 (0) | 2023.11.18 |
|---|---|
| [프로그래머스] [Python] (Level 2) 귤 고르기 (1) | 2023.11.18 |
| [프로그래머스] [Python] (Level 2) 두 원 사이의 정수 쌍 (0) | 2023.11.16 |
| [프로그래머스] [MySQL] (Level 2) 조건에 부합하는 중고거래 상태 조회하기 (1) | 2023.11.16 |
| [프로그래머스] [Python] (Level 2) 당구 연습 (+ 추가 test case) (1) | 2023.11.16 |